
https://school.programmers.co.kr/learn/courses/30/lessons/150367
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
2023.08.23 기준 Level 3
알고리즘 공부를 위해 풀고 기록하는 글입니다!
참고만 해주시고 더 좋은 풀이법이 있다면 알려주세요!
아이디어
- 10진수의 수가 주어짐
- 주어진 수를 2진수로 변환
- 이렇게 변환한 2진수로 포화 이진트리를 구성할 수 있는지 결과 리턴
진수 변환과 트리를 결합한 문제입니다.
우선 포화 이진 트리에 대해 알아야 했습니다.
포화 이진 트리는 이즌 트리이면서 서브트리까지 빈 곳 없이 노드가 존재하는 트리를 말합니다.
Full Binary Tree라고도 합니다.

이 문제에서는 우리가 임의로 포화 이진트리를 만들 수 있습니다.
이진수에서 0에 해당하는 수는 우리가 임의로 삽입한 노드이며 이 노드들을 삽입하여 포화 이진 트리를 만들고 이 트리를 Inorder로 나열한 것을 10진수로 변환한 것이 이 문제에서 제시한 이진트리로 수를 표현하는 방식입니다.
우선 우리에게 주어진 것은 10진수이기 때문에 이것을 2진수로 변환합니다.
이렇게 변환한 2진수를 이진 트리로 표현할 수 있으면 1을 아니면 0을 리턴하면 됩니다.
여기서 이진 트리는 결국 포화 이진트리를 의미합니다.
따라서
- 10진수를 2진수로 변환
- 변환한 2진수를 포화 이진 트리로 변환
- 포화 이진트리가 유효한지 검증
이 순서로 구현을 진행했습니다.
만약 주어진 수가 128이라면 이것의 2진수는 10000000 입니다.
이 2진수는 노드의 개수가 부족하기 때문에 포화 이진 트리를 구성할 수 없습니다.
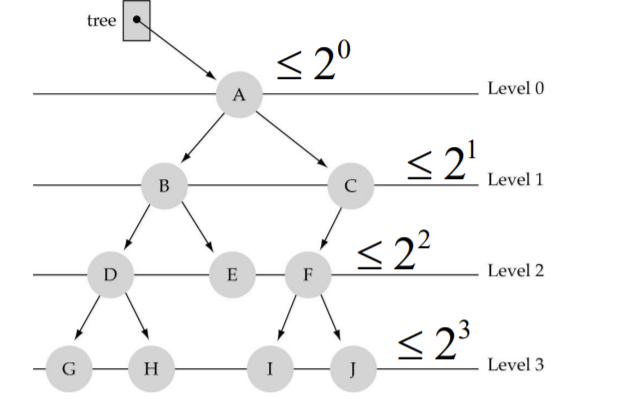
위는 이진 트리의 예시입니다. 트리는 루트부터 시작하여 각 depth별로 level로 나타낼 수 있습니다.
루트는 level 0이고 루트의 자식 노드는 level 1입니다.
이 때 각 레벨에 존재할 수 있는 노드의 개수는 최대 2^level 입니다.
즉, level 3에서는 2^3개까지의 노드가 존재 가능합니다.
포화 이진 트리에서는 level 3에서 2^3개의 노드가 전부 있어야 합니다.
포화 이진 트리에서 레벨 0~3까지의 총 노드 수는 2^0 + 2^1 + 2^2 + 2^3 = 15개입니다.

앞서 예시로 들었던 128 = 0b10000000은 2진수를 문자열로 나타냈을 때 크기인 8이 노드의 개수가 됩니다.
이 수는 어떠한 level의 포화 이진 트리 구성이 불가능합니다.
따라서 노드를 더 추가해줘야 하는데 원본인 128을 바꾸지 않고 2진수의 크기를 조절하는 방법이 있습니다.
바로, 2진수의 앞에 0들을 추가해주면 됩니다.
10000000과 010000000 or 00000010000000은 결국 10진수로 변환했을 때 똑같이 128이 나옵니다.
즉, 노드의 개수를 늘리고 싶다면 2진수의 앞쪽에 0을 필요한 만큼 넣으면 됩니다.
이제 추가해야할 노드의 개수를 구해야 합니다.
포화 이진 트리는 각 레벨별로 모든 노드가 꽉 차야 있어야 합니다.
트리의 높이 = H = 마지막 level + 1 이라고 했을 때,
포화 이진 트리의 특성을 이용해 level을 0부터 1씩 늘려가며 (H는 1부터 1씩 증가합니다.)
해당 H에서 포화 이진트리의 전체 노드 개수를 구합니다. (2^H - 1)
이렇게 구한 전체 노드 개수에서 현재 2진수의 노드 개수를 빼면 추가해야 할 0의 개수가 나오게 됩니다.
필요한 만큼 0을 앞에 넣어서 FullBinaryTree를 나타내는 2진수를 구합니다.
이제 이 포화 이진 트리가 유효한지 검증하는 단계입니다.
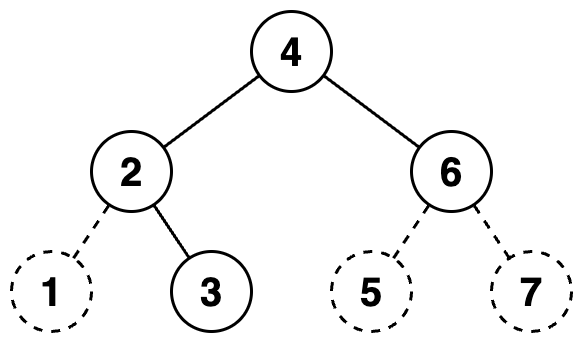
문제 조건에 따라 트리는 Inorder로 나열되게 되는데 위의 트리는 0111010을 나타냅니다. (점선은 임의로 추가한 노드이기 때문에 0)
여기서 규칙을 찾을 수 있는데 2진수에서 가운데에 해당하는 숫자가 트리의 루트가 됩니다.
그리고 해당 위치의 왼쪽 부분이 left subtree가 되고 오른쪽 부분이 right subtree가 됩니다.
abcdefg로 문자열이 있다면 d가 루트가 되고 abc | efg 이렇게 트리가 구성되는 구조입니다.
이렇게 나누어진 서브트리 abc와 efg는 또다시 중간을 기준으로 a, b, e, g로 나누어집니다.
즉, 문자열을 중앙 기준으로 좌측과 우측으로 나누어 재귀적으로 해당 서브트리들이 유효한지 검증하면 됩니다.
트리가 유효한 트리인지 검증하는 조건은 다음과 같습니다.
- 트리의 노드 개수가 2 이하면 true (더 이상 쪼갤 수 없기 때문)
- 트리의 루트가 1이면 true
- 트리의 루트가 0일 때 이 트리의 서브트리가 모두 0이면 true
3번의 조건이 중요했습니다. (이부분을 빼먹어서 고생했습니다...)
처음에는 트리의 루트가 0이면 루트를 임의로 삽입한 것이기 때문에 유효하지 않은 트리라고 생각했지만 아니었습니다.
루트가 0이어도 해당 루트의 자식들이 전부 0이라면 유효합니다. (문제 조건에서 리프 위치에만 더미 노드 삽입이 가능하다는 조건이 없기 때문에 리프 위치가 아니어도 0을 삽입할 수 있기 때문)
하지만 루트가 0인 상태에서 자식 중에 1이 있다면 이것은 불가능합니다.
원래도 이진 트리 상태였다가 더미 노드들을 넣어서 포화 이진 트리로 만들어야 하는데
루트가 0인데 자식 중에 1이 있다면 원래도 이진트리가 아니었다는 것이기 때문입니다.

이러한 포화 트리가 있을 때 푸른 영역인 left subtree는 유효합니다.
하지만 우측의 초록 영역의 right subtree가 불가능하기 때문에 올바른 트리가 아니라는 검증 결과가 나와야합니다.
이 트리에서 0들은 우리가 임의로 이진 트리에게 추가한 것인데 이 0을 넣기 전 상태가 다음과 같기 때문입니다.
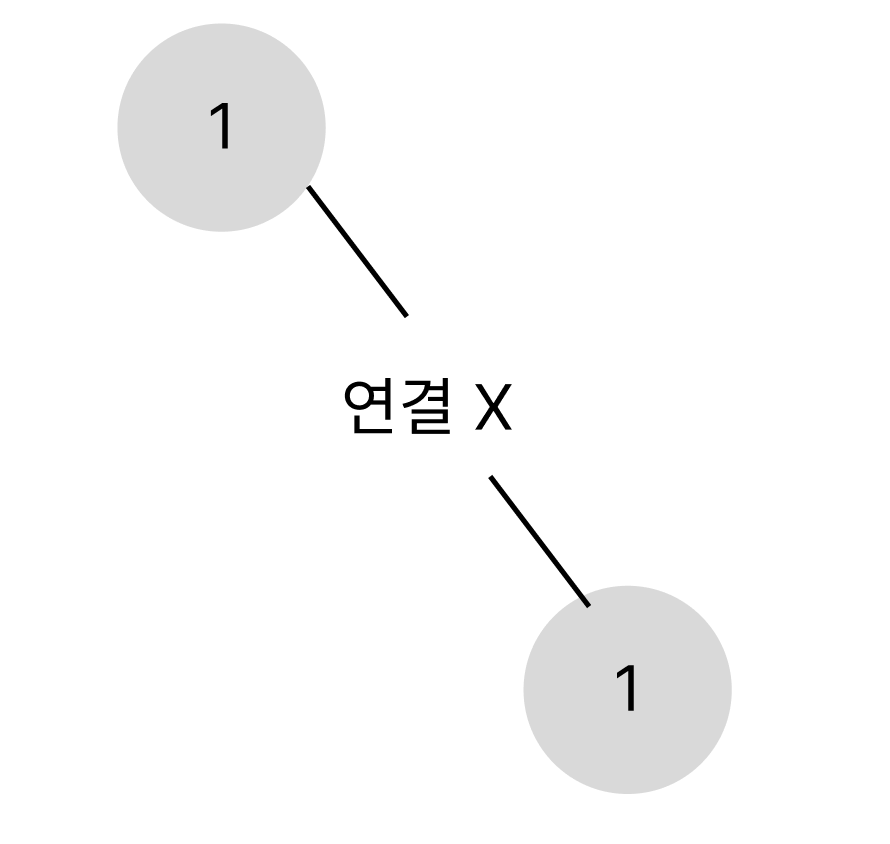
0인 노드를 제거했을 때 모습입니다. 애초에 1끼리 연결이 되어 있지 않아 이진 트리 자체가 아닌 상태였습니다.
원래 이진 트리일 때 0인 노드들을 추가로 삽입하여 포화 이진트리를 구성해야 하는데 이건 선후관계가 틀렸습니다.
따라서 루트가 0이고 자식 노드 중에 1이 있다면 해당 트리는 올바르지 않다고 판단하면 됩니다.
풀이
1. makeFullBinaryTree 함수 구현
// 노드의 개수와 트리의 level을 비교하여 포화 이진트리 만들기
fileprivate func makeFullBinaryTree(number: String) -> String {
var level: Double = 0
var nodeCnt = 1
while nodeCnt < number.count {
level += 1
nodeCnt += Int(pow(2, level))
}
let diff = nodeCnt - number.count // 이만큼 0을 앞에 추가해줘야 한다.
return String(repeating: "0", count: diff) + number
}2진수 문자열을 받아 포화 이진트리로 만들어서 리턴합니다. (0들을 앞에 추가)
2. isSubtreeZero 함수 구현
// 서브트리가 전부 0으로 구성되어 있는지 확인
fileprivate func isSubtreeZero(subree: String) -> Bool {
for num in subree {
if num == "1" {
return false
}
}
return true
}트리의 노드가 전부 0인지 확인하는 함수입니다.
3. canConvertBinaryTree 함수 구현
fileprivate func canConvertBinaryTree(num: String) -> Bool {
if num.count <= 2 {
return true
}
let middleIndex = num.index(num.startIndex, offsetBy: num.count / 2)
let leftSubtree = String(num[num.startIndex..<middleIndex])
let rightSubtreeStartIndex = num.index(after: middleIndex)
let rightSubtree = String(num[rightSubtreeStartIndex..<num.endIndex])
// 현재 검사중인 트리의 루트가 0인 경우
if num[middleIndex] == "0" {
// 서브트리가 모두 0이어야만 가능한 경우이다.
return isSubtreeZero(subree: leftSubtree) && isSubtreeZero(subree: rightSubtree)
}
return canConvertBinaryTree(num: leftSubtree) && canConvertBinaryTree(num: rightSubtree)
}포화 이진 트리를 파라미터로 받아서 유효한지 검증하는 함수입니다.
재귀적으로 동작합니다. (좌측 서브트리와 우측 서브트리가 모듀 유효하면 전체가 유효하다고 판단)
Swift에서 String을 인덱싱, 슬라이싱 하는 것이 살짝 불편합니다.
위의 코드에서처럼 offset으로 인덱스 타입에 해당하는 위치를 만들어줘야 합니다.
4. solution 함수 구현
fileprivate func solution(_ numbers:[Int64]) -> [Int] {
var result = [Int]()
for number in numbers {
let binaryNum = String(number, radix: 2)
let fullBinaryNum = makeFullBinaryTree(number: binaryNum)
let canConvert = canConvertBinaryTree(num: fullBinaryNum)
result.append(canConvert ? 1 : 0)
}
return result
}10진수를 2진수로 바꾸고 1번에서 만든 makeFullBinaryTree 함수로 포화 이진트리로 변환합니다.
그리고 canConvertBinaryTree로 유효한 트리인지 검증합니다.
마무리
저한테는 꽤 신선한 문제였습니다.
2진수와 트리에 대한 개념이 필요했습니다.
inorder이기 때문에 문자의 가운데가 루트인 것을 빠르게 파악했고 이 루트가 1일때는 자식 노드들이 무엇이든 유효하다는 사실을 알았지만 루트가 0이어도 자식들이 전부 0이면 유효하다는 사실은 파악하기 어려웠습니다.
또한 포화 이진 트리 형태로 변환하기 위해 0을 여러개 추가해야 할 수도 있다는 것을 놓쳤습니다.
2진수로 변환한 문자열이 짝수면 앞에 0을 1개만 붙여서 홀수개로 만들고 탐색을 했었는데 이렇게 하면 탐색 자체는 가능해지지만 애초에 포화 이진 트리가 아니기 때문에 당연히 문제 정답과 다른 답이 도출됩니다. (1번 테케만 성공)
'알고리즘' 카테고리의 다른 글
| [프로그래머스] Swift - N으로 표현 (0) | 2023.08.28 |
|---|---|
| [프로그래머스] Swift - 스타 수열 (0) | 2023.08.25 |
| [프로그래머스] Swift - 미로 탈출 명령어 (0) | 2023.08.22 |
| [프로그래머스] Swift - 110 옮기기 (0) | 2023.08.21 |
| [프로그래머스] Swift - 외벽 점검 (0) | 2023.08.17 |




댓글