
https://school.programmers.co.kr/learn/courses/30/lessons/60062
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
2023.08.17 기준 Level 3
알고리즘 공부를 위해 풀고 기록하는 글입니다!
참고만 해주시고 더 좋은 풀이법이 있다면 알려주세요!
아이디어
- 원형의 외벽 존재
- weak 배열에 취약 지점 데이터 제공
- dist에 친구들이 움직일 수 있는 거리 제공
- 최소의 인원으로 weak에 속한 지점들을 전부 수리할 때 필요한 인원수 리턴
간단해 보이지만 여러 요소들이 얽혀있어 최근에 풀었던 문제 중에 개인적으로 가장 어려웠습니다.
여러 방법을 시도해보다가 시간초과 + 몇몇 테케 실패로 인해 다른 분들의 풀이를 한번 보며 도움을 받았습니다.
우선 외벽이 원형으로 설계되어 있어 n을 넘어가는 위치에 가면 다시 0부터 시작하는 것을 고려해야 합니다.
또한 친구들을 배치할 때 어떤 지점을 시작 지점으로 하냐에 따라 커버하는 취약 지점의 수가 크게 달라집니다.
따라서 모든 경우의 수를 완전 탐색해야 했습니다.
다행히 weak는 15이하, dist는 8 이하로 크기가 작기 때문에 시간 복잡도 측면에서 제약이 크지 않았습니다.
먼저 원형구조는 weak 배열을 확장하여 해결했습니다.
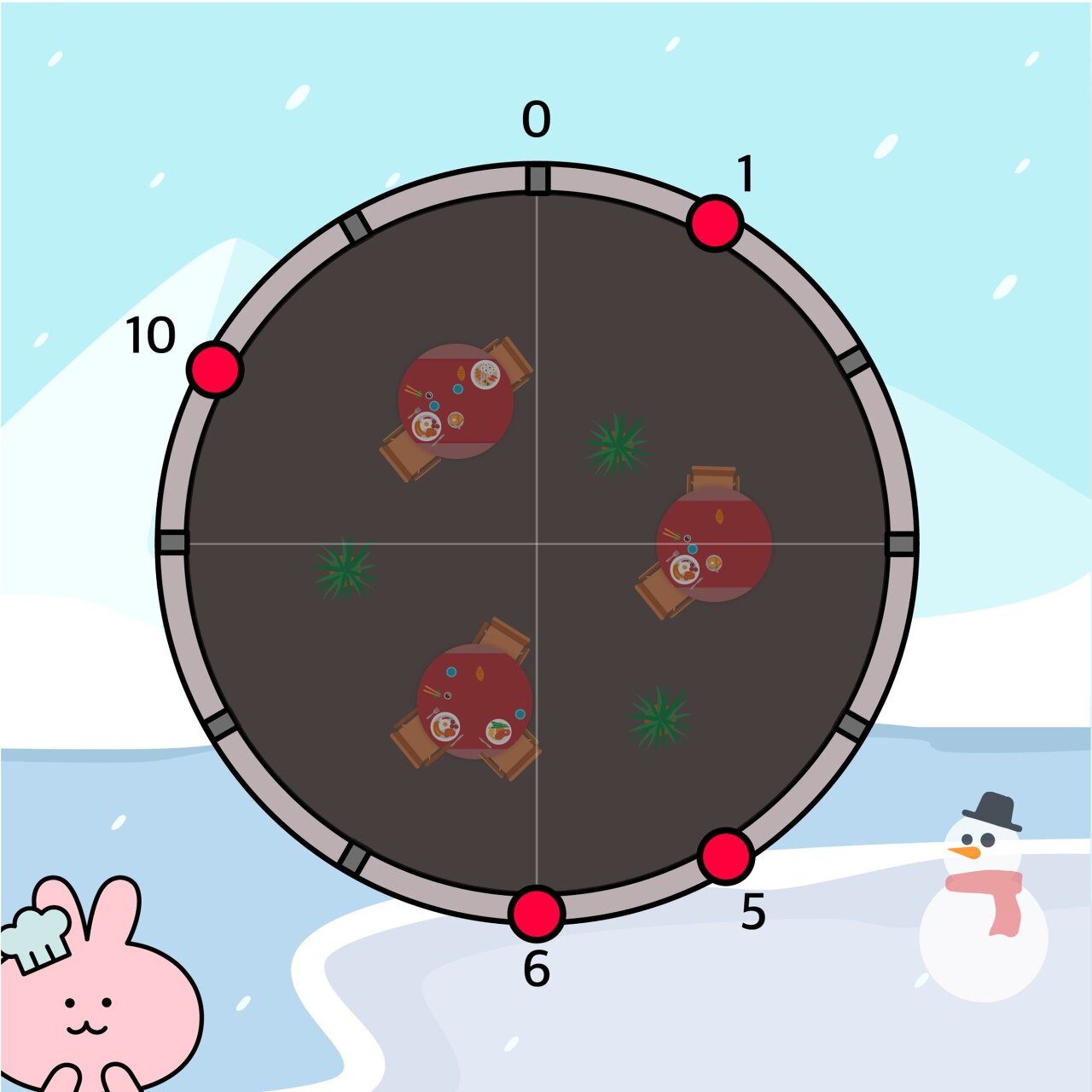
사진과 같은 구조에서 weak = [1, 5, 6, 10], n = 12 입니다.
이것을 확장한 extenedWeak = [1, 5, 6, 10, 13, 17, 18, 22] 를 만들었습니다.
기본 weak에 n을 각 요소에 더한 것들을 추가한 배열입니다.
이렇게 하면 12(n) 이상의 값을 접근할 때 나머지 연산 없이 다음 요소에 접근할 수 있습니다.
즉, 원형 구조를 선형 구조로 바꾸어 생각할 수 있습니다.
그 다음에 고려해야 하는 것은 시작 지점과 인원 투입 순서입니다.
위의 사진 예시의 상황에서 시작 지점에 따라 다양한 루트가 나옵니다.
1 -> 5 -> 6 -> 10
5 -> 5 -> 10 -> 1
6 -> 10 -> 1 -> 5
10 -> 1 -> 5 -> 6
이렇게 총 4가지의 루트가 존재합니다.
1 -> 6 -> 5 -> 10 과 같이 순서를 바꾼 루트는 여기서는 고려할 필요가 없습니다.
이후에 친구들을 순열을 통해 모든 경우의 수를 구하고 위의 4가지 루트에 대응하는 경우를 전부 탐색할 것이기 때문에 친구들을 순열하는 것이 루트의 순서를 뒤집는 작업을 대신하기 때문입니다.
결국 앞서 4가지의 루트가 나왔던것 처럼 문제에서 주어진 weak를 바탕으로 반복문을 통해 모든 루트를 찾고 해당 루트마다 친구들을 대응시켜서 모두 커버가 가능한지 확인하면 됩니다.
루트는 확장한 배열의 서브 배열입니다.
예시) route = [6, 10 ,13, 17], 이것은 곧 [6, 10, 1, 5]와 같기 때문에 모든 취약 지점을 포함합니다.
같은 루트라도 친구들이 투입되는 순서에 따라 커버 가능한 지점 수가 달라지기 때문에 한 루트마다 모든 친구들의 순서를 대응시켜서 확인해봐야합니다.
이를 위해 순열 (permutation)을 사용합니다.
친구들 배열(dist)에 순열을 취하여 순서를 고려한 모든 경우의 수를 구합니다.
이 경우의 수를 모든 루트에 적용시켜서 모든 취약 지점이 커버 가능한지 확인하면 됩니다.
풀이
1. permutation 구현
fileprivate func permutation<T: Comparable>(_ array: [T], _ n: Int) -> [[T]] {
var result = [[T]]()
if array.count < n { return result }
var stack: [([T], [Bool])] = array.enumerated().map {
var visited = Array(repeating: false, count: array.count)
visited[$0.offset] = true
return ([$0.element], visited)
}
while stack.count > 0 {
let now = stack.removeLast()
let elements = now.0
var visited = now.1
if elements.count == n {
result.append(elements)
continue
}
for i in 0...array.count-1 {
if visited[i] { continue }
visited[i] = true
stack.append((elements + [array[i]], visited))
visited[i] = false
}
}
return result
}스택을 활용한 순열 구현입니다.
2. solution 함수 구현
fileprivate func solution(_ n:Int, _ weak:[Int], _ dist:[Int]) -> Int {
var extendedWeak = weak
weak.forEach { extendedWeak.append($0+n) }
var result = dist.count + 1
let permutationResults = permutation(dist, dist.count)
for i in 0..<weak.count {
var route = [Int]()
for j in i..<(i+weak.count) {
route.append(extendedWeak[j])
}
for friends in permutationResults {
var cnt = 1 // 필요한 친구의 수
var coverLength = route[0] + friends[0] // 현재 친구까지의 커버 범위
for k in 0..<weak.count {
// 해당 친구가 커버할 수 있는 범위를 넘은 지점이 있는 경우
if route[k] > coverLength {
cnt += 1 // 다음 친구를 불러옴
if cnt > friends.count { // 친구의 수보다 더 사람이 필요한 경우 -> 불가능하기 때문에 탐색 중지
break
}
coverLength = route[k] + friends[cnt-1]
}
}
result = min(result, cnt)
}
}
if result > dist.count {
return -1
}
return result
}weak를 확장한 extendedWeak를 먼저 생성했습니다.
순열로 순서에 상관 있게 친구들을 나열한 리스트를 구합니다.
반목문으로 가능한 모든 루트를 탐색합니다.
순열로 얻은 값들을 순회하며 해당 루트와 친구를 나열한 배열에서 모든 지점을 점검할 수 있는지 파악합니다.
코드의 주석을 참고해주세요!
마무리
어려웠습니다..
고려해야할 것도 많고
다른 사람들의 답안을 봐도 쉽게 이해되지 않았습니다.
그나마 잘 이해가 되는 답안을 참고하여 문제를 풀었습니다.
1. 원형 구조가 주어지면 배열을 확장하여 선형 구조로 변경
2. 주어진 변수의 크기가 작다면 완전 탐색을 고려
3. 순열을 사용하여 완전 탐색
'알고리즘' 카테고리의 다른 글
| [프로그래머스] Swift - 미로 탈출 명령어 (0) | 2023.08.22 |
|---|---|
| [프로그래머스] Swift - 110 옮기기 (0) | 2023.08.21 |
| [프로그래머스] Swift - 양과 늑대 (0) | 2023.08.16 |
| [프로그래머스] Swift - 광고 삽입 (0) | 2023.08.15 |
| [프로그래머스] Swift - 인사고과 (0) | 2023.08.11 |




댓글