
https://school.programmers.co.kr/learn/courses/30/lessons/67259
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
2023.07.24 기준 Level 3
알고리즘 공부를 위해 풀고 기록하는 글입니다!
참고만 해주시고 더 좋은 풀이법이 있다면 알려주세요!
아이디어
2차원 배열 지도를 탐색해서 최소 비용을 찾는 문제이기 때문에 DFS, BFS를 통한 풀이법을 떠올렸습니다.
처음에 DFS로 풀어보다가 시간 초과가 발생하여 BFS로 변경했습니다.
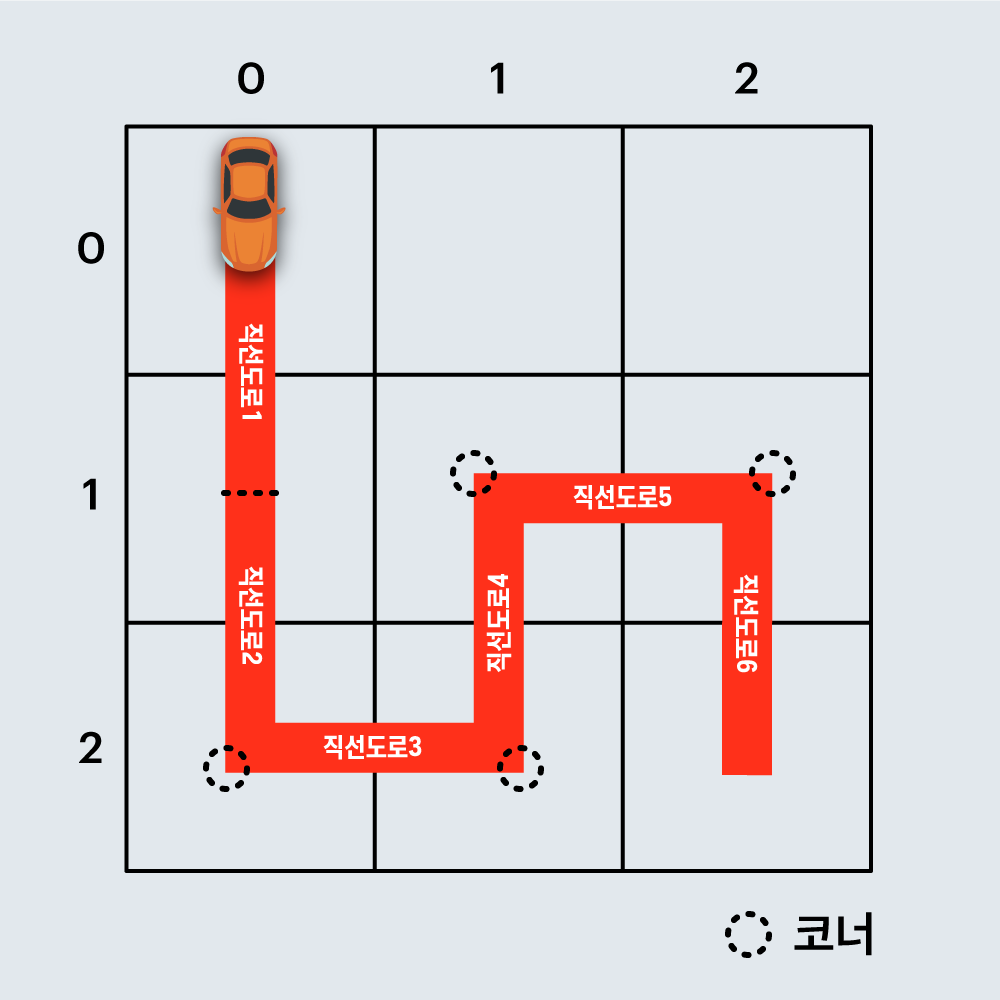
이 문제의 핵심 요구 사항은 코너부분입니다.
코너를 만들게 되면 비용이 직선 경로보다 6배 증가하기 때문에 비용을 계산할 때 코너를 잘 고려해야 합니다.
코너는 어떤 방향으로 진입하냐에 따라 생길 수도 있고 안 생길 수도 있습니다.
위의 사진에서 (2, 1)위치로 갈 때 (1, 1)에서 진입을 했습니다.
이때 (1, 1)로 향하는 방향이 북쪽이었기 때문에 동쪽인 (2, 1)로 경로를 만들었을 때 코너가 생겼습니다.
만약 (1, 1)로 향하는 방향이 같은 동쪽이었다면 ((0, 1)에서 (1, 1)로 진입하는 경로였다면)
코너가 생기지 않았다는 의미입니다!
즉 같은 위치까지의 경로를 구할 때 어떤 방향으로부터 진입하냐에 따라 소용 비용이 달라질 수 있습니다.
따라서 (x, y)까지의 최소 비용을 저장할 때 동서남북 중 어떤 방향으로부터 왔을 때의 최소 비용인지 구분해서 저장해야 합니다.
이를 위해 3차원 배열을 사용합니다.
이 배열의 이름을 distance라고 한다면 distance[방향][x][y] 형태로 (x, y)까지의 각 방향별 최소 비용을 저장하며 BFS를 진행하는 것입니다.
풀이
1. 큐 구현
우선 BFS를 위해 큐를 구현합니다. Swift의 어레이에 직접 append, removeFirst를 사용해도 무방합니다.
스택을 2개 사용하여 큐를 구현하여 시간 복잡도를 낮출 수 있지만 아래와 같이 구현해도 테스트 케이스를 통과하는 것을 확인했습니다.
import Foundation
public struct Queue<T> {
// MARK: - Properties
private var info = [T]()
/// O(1)
public var count: Int {
self.info.count
}
/// O(1)
public var isEmpty: Bool {
self.info.isEmpty
}
/// O(1)
public var peek: T? {
self.info.first
}
// MARK: - initialization
public init() {}
// MARK: - Methods
/// O(1)
public mutating func enqueue(_ item: T) {
self.info.append(item)
}
/// O(n)
@discardableResult
public mutating func dequeue() -> T? {
return self.info.removeFirst()
}
}
2. Point 구조체 구현
좌표를 저장할 구조체를 생성합니다. 이 구조체의 객체가 큐에 들어가게 됩니다.
방향!!을 저장해야 하기 때문에 direction 속성을 추가했습니다.
fileprivate struct Point {
let x: Int
let y: Int
let cost: Int
let direction: Int
}
3. solution 함수 구현
fileprivate func solution(_ board:[[Int]]) -> Int {
let n = board.count
let dx = [1, -1, 0, 0]
let dy = [0, 0, -1, 1]
// 3차원 어레이 [방향][X][Y]
var distance = Array(repeating: Array(repeating: Array(repeating: Int.max, count: n), count: n), count: 4)
func bfs() {
var queue = Queue<Point>()
// (0, 0)의 좌표를 동서남북 4개의 방향으로 갈 때의 초기값을 큐에 넣는다.
for direction in 0..<4 {
queue.enqueue(Point(x: 0, y: 0, cost: 0, direction: direction))
distance[direction][0][0] = 0
}
while !queue.isEmpty {
let current = queue.dequeue()!
let x = current.x
let y = current.y
let prevDirection = current.direction
for i in 0..<4 {
let nextX = x + dx[i]
let nextY = y + dy[i]
// 이전 위치로 다시 돌아가는 경우는 제외시킴
if nextX == x && nextY == y {
continue
}
if nextX >= 0 && nextX < n && nextY >= 0 && nextY < n && board[nextY][nextX] == 0 {
let isCorner = checkIsCorner(direction: i, prevDirection: prevDirection)
let nextCost = isCorner ? current.cost + 600 : current.cost + 100
if distance[i][nextY][nextX] > nextCost {
distance[i][nextY][nextX] = nextCost
queue.enqueue(Point(x: nextX, y: nextY, cost: nextCost, direction: i))
}
}
}
}
}
bfs()
var result = Int.max
// 동서남북의 방향 중에서 목적지까지의 최소 비용을 답으로 정한다.
for i in 0..<4 {
result = min(result, distance[i][n-1][n-1])
}
return result
}
fileprivate func checkIsCorner(direction: Int, prevDirection: Int) -> Bool {
return direction != prevDirection
}(x, y)까지의 최소 비용을 저장할 때는 항상 동서남북 중 어떤 방향으로 도착한 것인지 저장해야 합니다.
이 방향은 Int값으로 관리합니다.
다만 직전의 좌표로 다시 돌아가는 경로(방향)는 중복 계산할 필요가 없기 때문에 if문으로 제외시켜 주었습니다!
마무리
베이스는 일반적인 BFS 탐색으로 최소 비용을 구하는 것이지만 추가적으로 코너라는 개념이 더해져 1단계 더 난이도가 높아진 문제였습니다.
코너 때문에 각 좌표까지 이동한 방향을 고려해야 했고 이 방향에 따른 최소 비용을 따로 기록하기 위해 3차원 배열을 사용했습니다.
'알고리즘' 카테고리의 다른 글
| [프로그래머스] Swift - 가장 긴 팰린드롬 (0) | 2023.07.26 |
|---|---|
| [프로그래머스] Swift - 입국심사 (0) | 2023.07.25 |
| [프로그래머스] Swift - 합승 택시 요금 (0) | 2023.07.23 |
| [프로그래머스] Swift - 디스크 컨트롤러 (0) | 2023.07.21 |
| [프로그래머스] Swift - 여행경로 (0) | 2023.07.19 |




댓글