
https://school.programmers.co.kr/learn/courses/30/lessons/258705
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
2024.01.18 기준 Level 3
알고리즘 공부를 위해 풀고 기록하는 글입니다!
참고만 해주시고 더 좋은 풀이법이 있다면 알려주세요!
아이디어
문제 조건
- 한 변의 길이가 1인 정삼각형 2n+1 개를 이어 붙여 윗변의 길이가 n, 아랫변의 길이가 n+1인 사다리꼴을 만들 수 있다.
- 사다리꼴의 윗변과 변을 공유하는 n개의 정삼각형 중 일부의 위쪽에 같은 크기의 정삼각형을 붙여 새로운 모양을 만든다.
- 이렇게 만든 모양을 정삼각형 타일 또는 정삼각형 2개를 이어 붙여 만든 마름모 모양 타일로 빈곳이 없도록 채우려고 한다. (타일을 돌려서 사용 가능)
- 타일을 빈 곳 없이 채워 넣는 경우의 수를 10007로 나눈 나머지를 리턴하자
- n과 tops가 주어진다.
이번 문제는 산 모양 타일링의 규칙을 찾아서 DP로 풀어야 하는 문제였습니다.
코드 자체는 간단하지만 개인적으로 이 아이디어를 떠올리는 것이 매우 어려웠습니다. (카카오 정답 해설을 참고했습니다.)
우선 포인트는 아래 방향 정삼각형을 기준으로 타일을 늘려가며 경우의 수를 계산하는 것입니다.

사진에서 동그라미 친 부분이 아래 방향 정삼각형입니다.
이 삼각형을 타일로 채우는 방법은 총 4가지 입니다.
아래 방향 정삼각형을 기준으로
- 위쪽 정삼각형과 함께 마름모 타일로 덮기 (위쪽 정삼각형이 있는 경우)
- 왼쪽 정삼각형과 함께 마름모 타일로 덮기
- 오른쪽 정삼각형과 함께 마름모 타일로 덮기
- 그냥 정삼각형 타일로 자신만 덮기
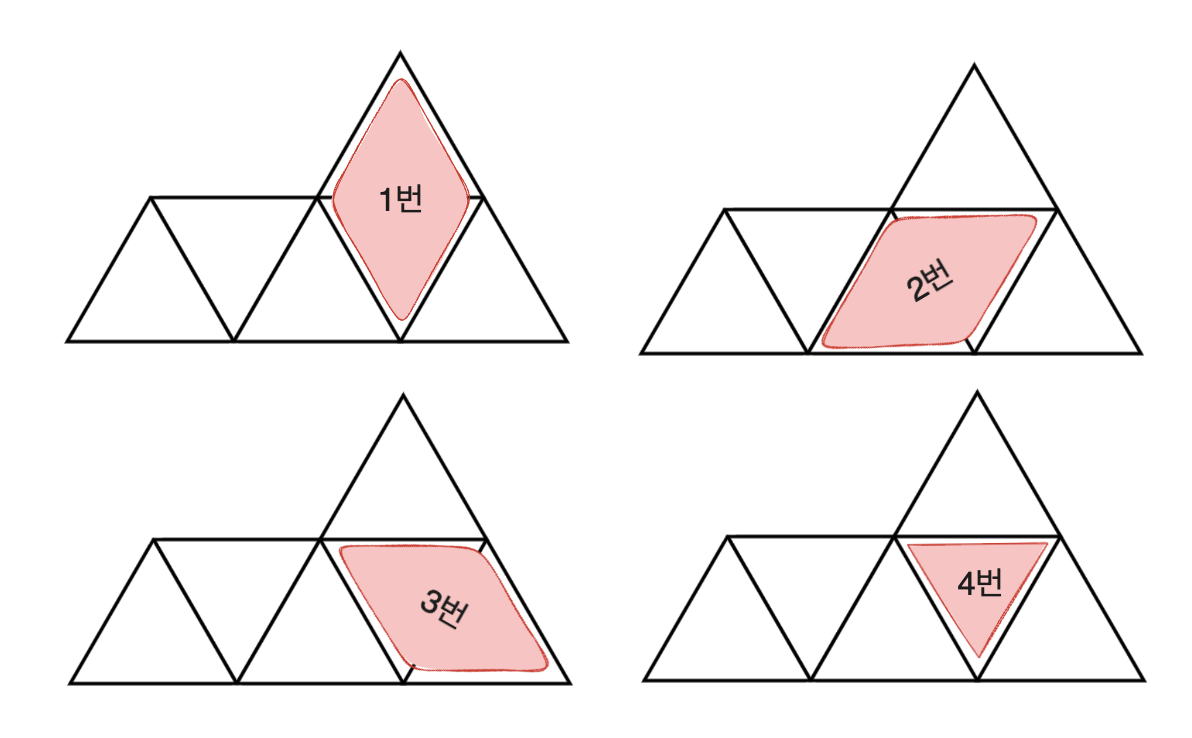
2번 째 아래방향 삼각형을 기준으로 각 방법들을 그림으로 나타내면 위와 같습니다.
이제 규칙을 찾아볼 수 있습니다.
- 1번 방법은 위쪽 정삼각형이 있는 경우에서만 가능
- 이전 아래 방향 정삼각형에 3번 방법을 적용했다면 현재 계산하고자 하는 아래 방향 정삼각형에는 2번 방법을 사용할 수 없다.
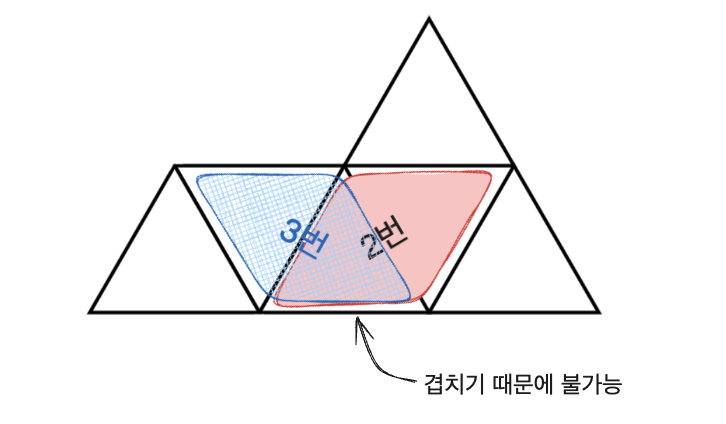
따라서 2개의 DP 배열을 생성하여 3번 방법을 사용했을 때와 아닐 때를 분리해서 경우의 수를 계산해야 합니다.
카카오 해설에서는 a, b 배열로 선언했는데 저는
withThirdWay와 withoutThridWay로 이름 붙였습니다.
withThirdWay[i]는 i번째 아래 방향 삼각형까지 덮되, 3번 방법만 사용할 때의 경우의 수
withoutThridWay[i]는 i번째 아래 방향 삼각형까지 덮되, 3번 방법을 사용하지 않을 때의 경우의 수
를 의미합니다.
이제 점화식을 세울 수 있습니다.
i번째 아래 방향 정삼각형 위에 정삼각형이 붙은 경우 (tops[i-1] == 1)
- withThirdWay[i] = withThirdWay[i-1] + withoutThirdWay[i-1]
3번 방법을 사용해야 하는데 이전 타일까지 3번 방법을 사용한 경우의 수와 3번 방법을 사용하지 않았던 경우의 수를 그대로 더해주면 됩니다.
- withoutThirdWay[i] = 2 * withThirdWay[i-1] + 3 * withoutThirdWay[i-1]
3번 방법을 사용하지 않고 타일을 채우는 방법은 1,2,4번 방법이기 때문에 총 3가지입니다.
이전 아래 방향 타일까지 3번 방법을 사용했다면 1,4번 방법만 가능하기 때문에 2를 곱해주고,
이전 아래 방향 타일까지 3번 방법을 사용하지 않았다면 1,2,4번 방법 모두 가능하기 때문에 3를 곱해줍니다.
(withoutThirdWay을 채우는 것이기 때문에 3번 방법의 사용은 제외하고 계산해야 합니다.)
i번째 아래 방향 정삼각형 위에 정삼각형이 붙지 않은 경우 (tops[i-1] == 0)
- withThirdWay[i] = withThirdWay[i-1] + withoutThirdWay[i-1]
마찬가지로 3번 방법을 사용해야 하는데 이전 타일까지 3번 방법을 사용한 경우의 수와 3번 방법을 사용하지 않았던 경우의 수를 그대로 더해주면 됩니다.
- withoutThirdWay[i] = withThirdWay[i-1] + 2 * withoutThirdWay[i-1]
3번 방법을 사용하지 않고 타일을 채우는 방법은 1,2,4번 방법이기 때문에 총 3가지입니다.
이전 아래 방향 타일까지 3번 방법을 사용했다면 4번 방법만 가능하기 때문에 1을 곱해주고,
이전 아래 방향 타일까지 3번 방법을 사용하지 않았다면 2,4번 방법 모두 가능하기 때문에 3를 곱해줍니다.
그리고 경우의 수가 매우 커지기 때문에 DP 배열을 채울 때마다 10007의 나머지 연산을 해주는 것을 잊으면 안 됩니다!
이렇게 전부 배열을 채우고
(withThirdWay[n] + withoutThirdWay[n]) % 10007
을 리턴하면 정답입니다.
풀이
solution 함수 구현
fileprivate func solution(_ n:Int, _ tops:[Int]) -> Int {
var withThirdWay = Array(repeating: 0, count: n+1) // 3번 방법으로만 채울 수 있는 경우의 수
var withoutThirdWay = Array(repeating: 0, count: n+1) // 3번 방법을 제외하고 채울 수 있는 경우의 수 (1,2,4번 방법)
withThirdWay[1] = 1
withoutThirdWay[1] = tops[0] == 1 ? 3 : 2
if n == 1 {
return withThirdWay[1] + withoutThirdWay[1]
}
let mod = 10007
for i in 2..<n+1 {
if tops[i-1] == 1 { // 위에 삼각형이 붙은 경우
withThirdWay[i] = withThirdWay[i-1] + withoutThirdWay[i-1]
withoutThirdWay[i] = 2 * withThirdWay[i-1] + 3 * withoutThirdWay[i-1]
} else { // 위에 삼각형이 붙지 않은 경우
withThirdWay[i] = withThirdWay[i-1] + withoutThirdWay[i-1]
withoutThirdWay[i] = withThirdWay[i-1] + 2 * withoutThirdWay[i-1]
}
withThirdWay[i] %= mod
withoutThirdWay[i] %= mod
}
return (withThirdWay[n] + withoutThirdWay[n]) % 10007
}
마무리
최근 카카오 인턴 코테에 나왔던 문제였습니다.
저도 이 시험에 참여를 했었는데 이 문제는 마지막 문제라 사실 시도조차 못했던 문제입니다.
현재 프로그래머스에서는 정답률이 다른 문제 보다 높던데, 아마 풀이 코드 자체는 간단해서라고 생각됩니다. (해설을 보면 조금만 타이핑해도 정답 가능)
하지만 문제 난이도 자체는 높았다고 생각합니다.
타일에서부터 규칙을 찾고 아래 방향 정삼각형을 기준으로 DP 를 사용한다는 아이디어를 떠올리는 것은 매우 허들이 높다고 느껴집니다.
그래도 해설을 보면 풀이 이해가 금방 되는 문제였습니다.
'알고리즘' 카테고리의 다른 글
| [프로그래머스] Swift - 주사위 고르기 (0) | 2024.01.22 |
|---|---|
| [프로그래머스] Swift - 고고학 최고의 발견 (0) | 2024.01.19 |
| [프로그래머스] Swift - 상담원 인원 (1) | 2024.01.15 |
| [프로그래머스] Swift - 사라지는 발판 (1) | 2024.01.14 |
| [프로그래머스] Swift - 퍼즐 조각 채우기 (0) | 2024.01.12 |




댓글